MEMS器件机电一体化相关研究进展

1 准静态吸合电压的物理模型

图1 非线性机电耦合系统。

如图1所示，当梁与衬底之间存在电势差，即驱动电压时，静电引力将梁向下吸引，而梁的弹性回复力，即弹力，将梁向上回复。简言之，静电引力和弹性回复力保持平衡状态。然而，梁的变形会导致其表面电荷分布的变化，从而电场将重新分布并作用于梁上，直到达到新的平衡状态。因此，图1是一个非线性机电耦合系统。图12示出了静电力和弹力随梁变形的变化规律。

图 2.电压控制平行板静电致动器的电力和弹簧力。

横坐标是梁的变形（g0 -g）与梁和基底之间的初始间隙（g 0）的比值，纵坐标是力。弹簧力与梁的变形成正比，而静电力，即电力，与变形的平方成正比。当驱动电压较小时，弹簧力可以与静电力抗衡，使系统处于稳定的平衡状态。然而，当驱动电压达到一个临界值时，弹簧力不再能与静电力抗衡，使梁失去平衡。驱动电压的临界值称为吸合电压。在吸合时，系统处于不稳定的平衡状态。图1的物理模型可以用图3所示的分析模型来建模，该模型由一个由弹簧悬挂的平行板电容器组成。当变形超过平行板初始间隙的三分之一时，就会发生吸合。因此，分析MEMS器件的机电性能的关键是研究其准静态吸合特性。

图 3.等效弹簧和平行板电容器的离散模型。

1994 年至 1997 年，Senturia等发表了一系列针对 MEMS 器件机电一体化的研究成果。1994 年，Senturia 将静电力驱动的微桥形梁模拟为等效弹簧和平行板电容器的集总模型（图3），得到了吸合电压、几何尺寸和材料参数的基本函数形式。1997 年，他们提出了 M-Test 技术，利用半导体工艺技术制作了三种不同的微测试结构，分别是微悬臂梁、微桥形梁和微扇形板，并制作不同长度的微梁分别测量其吸合电压，以便根据测量数据和模拟数概括校正因子，最终在离散模型的基础上修改了函数形式。2002 年，Pamidighantam等将该系统模拟为等效弹簧和平行板电容器的离散系统，利用商业仿真软件CoventorWare获取等效弹簧的刚度和平行板电容器的等效面积，从而得到微桥梁的吸合电压关系，但偏差高达18%。2003年，O'Mahony等也利用CoventorWare分析了静电载荷下的微桥梁，考虑边缘电容效应、板状现象的效率以及不同的边界条件，推导出微桥梁的数值解。2005年，Lishchynska等[95 ]利用CoventorWare仿真软件推导出悬臂梁吸合电压的数值解，误差在4%以内。2004年至2008年，Krylov等利用CoventorWare仿真软件对微桥梁进行了数值计算，得到了微桥梁的吸合电压。发表了一系列关于微结构拉入行为的研究成果。2004年，Krylov等研究了静电力作用下微梁的瞬态非线性动力学，建立了基于Galerkin程序的正则模态模型，该模型考虑了分布非线性静电力、非线性压缩膜阻尼和梁所带质量块的转动惯量的影响。2006年，Krylov等利用微扰理论，建立了静电压力的简单表达式，并进行了高阶修正，主要与电极的曲率和斜率有关。结果表明，调整机械压力的比例，弦具有不同的吸合行为。在较小的初始预应力情况下，出现弦的双稳态。2008 年，Krylov等人报道了在分布静电力作用下初始弯曲的双夹紧微梁中的多稳态现象的理论和实验研究。结果表明，具有初始弯曲柔性的双夹紧微梁的吸合电压低于直梁。从 2006 年到 2009 年，Hu 等人提出了一个近似分析模型，考虑了诸如初始应力、边缘电容效应和弹性边界等因素。例如，文献提出了一种具有弹性边界的微桥吸合电压的近似解析模型，微桥的弹性边界可以看作两端带有扭转弹簧的梁，微桥的概念图如图4所示。

图 4.（a）物理模型，（b）分析模型。

梁的长度为L，锚杆的高度为La，宽度为b，厚度为h，初始间隙为g，在驱动电压V的作用下，梁产生与位置相关的挠度w( x )。等效扭转弹簧常数k可用下式表示：

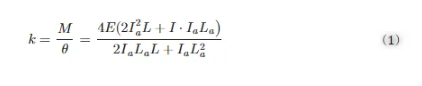
其中，I表示面积惯性矩，下标a表示锚点，E表示杨氏模量。反作用弯矩M和旋转角θ由承受均布载荷P0 的框架推导出来，如图 5所示：

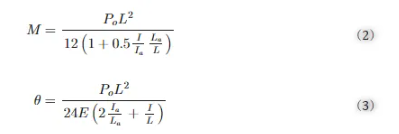
图 5（a）框架承受分布载荷 P0，（b）自由体图 。

基于欧拉梁模型和最小能量法，微桥的吸合电压VPI 为：

其中σ0表示初始应力，φ表示两端带有扭转弹簧的梁的第一固有模态，公式如下 ：

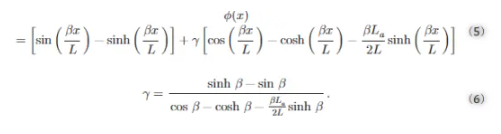
此外，β还应满足下列公式：

方程（4）具有明显的物理意义。第一项表明吸合电压取决于初始残余应力，第二项取决于梁的柔韧性，第三项取决于弹性边界条件。这些发现比我们上文提到的那些在MEMS器件机电研究中采用数值方法的研究结果具有更显著的物理意义。

2 微观结构动态响应分析

梁在运动过程中受到静电力、弹性回复力和阻尼力相互作用的影响，耦合运动方程往往是静电力方程、欧拉梁方程和空气阻尼方程的联立偏微分方程，以解释器件在三维空间中的动态行为。单纯用数值方法求解该方程非常困难，因此通常采用状态变量分析、基函数展开等数学运算，将无限维偏微分方程转化为有限维常微分方程组，即降阶方法。Younis等提出了一种降阶模型来分析静电力驱动微梁的行为。该模型是利用 Galerkin 法将分布参数系统离散为有限自由度系统得到的，其中考虑了中等大挠度、动载荷、线性与非线性弹性恢复力、电容器产生的非线性静电力以及机械力与静电力的耦合等影响。然而，在降阶方法下，当考虑空气阻尼时，器件的动态行为分析会非常困难，而其他相关参数仍需通过数值方法获得，分析效率并未提高。针对这一问题，Clark 提出了一种分析 MEMS 器件动态行为的有效方法，即将复杂系统划分为若干个基本结构单元，然后利用相似系统之间的仿真协议建立由这些基本结构组成的等效电路模型。Wen 采用基于偏置点附近线性化的模型分析方法来分析梁频域中的交流小信号。张将静电驱动悬臂梁等效为单自由度模型，建立其解析模型，并采用反馈机制实现耦合，进行时域和频域分析。时域分析中，驱动电压越大，悬臂梁的超调越明显；频域分析中，随着驱动电压的增加，悬臂梁的固有频率逐渐降低。胡建立了静电驱动器件的动态特性与稳定性分析模型，发现微结构的刚度会随着施加电压的频率周期性地软化，且刚度的变化量随着施加电压的大小而增大（图6）。

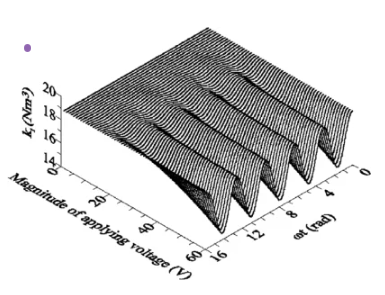
图 6.一阶模态刚度变化。

动态吸合电压可能低于静态吸合电压（图7）。

图 7.动态不稳定性与静态拉入的比较。

此外，如图8中的点状区域所示，动态拉近的不稳定区域随着施加电压的增加而扩大。如果结构在小变形条件下作用，则可以将梁视为线性的。相反，对于大变形，则必须考虑非线性结构效应。为了解决非线性问题，可以使用有限元分析 (FEA) 来获得非线性三次项。此外，这将有助于预测非线性机械刚度行为。具有三次刚度非线性的振动系统的控制方程可以写成：

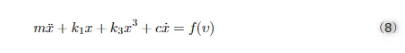
其中，c、f ( v )、m、k1、k3和x分别代表等效阻尼系数、取决于驱动电压v的等效外部周期力、等效质量、等效线性刚度系数、等效非线性刚度系数和变形。

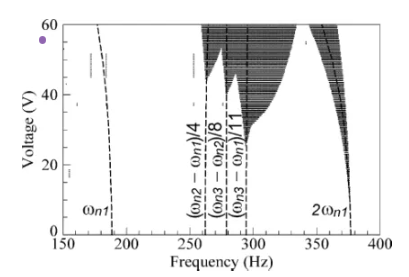
图 8.交流电压作用下微悬臂梁的动态不稳定区域。

免责申明：所有信息均源于网络，相关内容仅供参考学习，所有转载及汇编内容，均不代表本公众号赞同其观点，不能完全保证其真实性。如若本网站无意侵犯媒体或个人知识产权，请私信联系，我们将立即予以删除。